So today I decided to compute the probabilities involved and the expected number of draws until I find a matching pair.
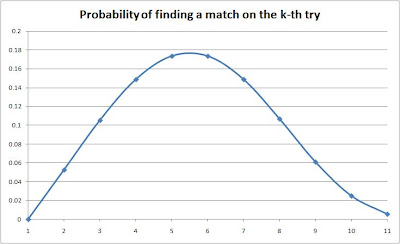
I draw one sock at a time uniformly at random until I have a matching pair. If I have 10 pairs of socks (all of them different), the probabilities of drawing a sock exactly at the k-th draw are as follows:
p(1 draw) = 0 (can't have a pair with only one sock)
p(2 draws) = (1 / 19) (I have 1 sock in my hands and I can draw any of the other 19 socks)
p(3 draws) = (1 - p(2)) * (2 / 18) (To get here, I can't have drawn a pair in the previous two draws; and now I have 2 socks and I can draw any of the other 18 socks)
...
p(10 draws) = (1 - p(2) - p(3) - ... - p(9)) * (9 / 11)
p(11 draws) = (1 - p(2) - p(3) - ... - p(9) - p(10)) * (10 / 10) (To get here, I can't have drawn a pair in the previous ten draws; I've also got all possible socks so anything that I draw at this point will match one of them, so the probability of finding a match here is 1)
The expected number of draws to find a matching pair is:
1 * p(1) + 2 * p(2) + 3 * p(3) + ... + 10 * p(10) + 11 * p(11)
That gives around 5.7 draws.
Ok, I don't feel as bad now. I still feel the universe is playing tricks on me, but at least they're subtle enough to keep my paranoia at bay.
Bonus: a graph showing the probabilities of finding a match on the k-th try.
10 comments:
I have the perfect solution that avoid all this problem
Have the same model for all your socks. But if you want different kinds, use different colors for each model, this way your color perception will considerably improve your selection.
I was just about to comment the same thing Hermann did. BUT you are not taking into account that you can LOOK inside the dryer when drawing socks! Or do you really "draw one sock at a time uniformly at random until you have a matching pair"??
BTW, you are SUCH a nerd :D
On a random note, I am going to start working as a Business Analyst for Dell, starting next month. Yay! :D
All models are simplifications; you can't expect mine to be any different.
HOWEVER, given that I wash/dry my clothes in batch, usually there's a ton of other stuff in the dryer. Hence it's pretty usual for me to only find one sock at a time.
Sure. Estava apenas implicando. Tu estás muito nerd mesmo, só comentaste a parte das meias e nem deu bola para o meu comentário da mudança de emprego :P
The socks problem has a generalization for creatures with more than two feet. Thiago's approach does not work, but the problem is now completely solved, after much very nerdy work, and it's mathematically very interesting. A write-up is available from me.
JJM: who are you? :)
James Madden, LSU Dept. Math.
Awesome. I didn't mean to be rude, I was just curious. How did a professional mathematician end up on this page? :)
Did you post your n-feet generalization anywhere? I'd love to take a look.
I treat my socks the same way Thiago does, and I got interested in the problem for the same reason he did. It proved to be more interesting that I originally expected. See: http://www.math.lsu.edu/~madden/socks12-12-09.pdf
I found Thiago's blog when I started wondering if other people besides me had the same interest, and I googled "socks, dryer, match, probability" or something like that.
Wow, thanks for sharing this. This is truly helpful. There is another really effective solution, as well.
http://www.ryanboatright.com/matchingsocks
Post a Comment