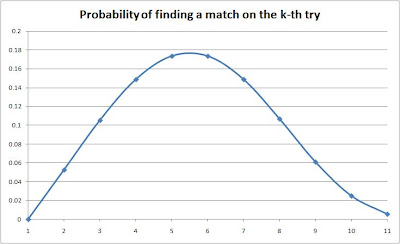
So today I decided to compute the probabilities involved and the expected number of draws until I find a matching pair.
I draw one sock at a time uniformly at random until I have a matching pair. If I have 10 pairs of socks (all of them different), the probabilities of drawing a sock exactly at the k-th draw are as follows:
p(1 draw) = 0 (can't have a pair with only one sock)
p(2 draws) = (1 / 19) (I have 1 sock in my hands and I can draw any of the other 19 socks)
p(3 draws) = (1 - p(2)) * (2 / 18) (To get here, I can't have drawn a pair in the previous two draws; and now I have 2 socks and I can draw any of the other 18 socks)
...
p(10 draws) = (1 - p(2) - p(3) - ... - p(9)) * (9 / 11)
p(11 draws) = (1 - p(2) - p(3) - ... - p(9) - p(10)) * (10 / 10) (To get here, I can't have drawn a pair in the previous ten draws; I've also got all possible socks so anything that I draw at this point will match one of them, so the probability of finding a match here is 1)
The expected number of draws to find a matching pair is:
1 * p(1) + 2 * p(2) + 3 * p(3) + ... + 10 * p(10) + 11 * p(11)
That gives around 5.7 draws.
Ok, I don't feel as bad now. I still feel the universe is playing tricks on me, but at least they're subtle enough to keep my paranoia at bay.
Bonus: a graph showing the probabilities of finding a match on the k-th try.